Тепловые расчеты процессов холодильной технологии пищевых продуктов могут быть выполнены только в том случае, если известны теплофизические характеристики этих продуктов и их зависимость от температуры.
Наиболее важные теплофизические характеристики пищевых продуктов:
удельная теплоемкость с [Дж/(кг · К)];
коэффициент теплопроводности λ [Вт/(м · К)];
коэффициент температуропроводности а (м2/с);
плотность продукта ρ (кг/м3).
При этом
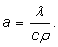
(1.1)
К теплофизическим характеристикам относят температуру начала замерзания пищевых продуктов, называемую криоскопической температурой tкр (°C); теплоту кристаллизации влаги r (Дж/кг), а также некоторые менее употребительные, такие, как теплота затвердевания жиров в продукте и теплота дыхания растительных продуктов.
Теплофизические характеристики продуктов зависят от их природных свойств (состава, строения). Различия свойств продуктов определяются их химической и физической неоднородностью. Химическая неоднородность зависит от состава продукта, физическая - от структуры и стереометрического распределения отдельных составных частей в продукте. В понятие структуры включают размер и направление волокон у животных продуктов, пористость, размер клеток и распределение газовых включений у растительных продуктов. Различие теплофизических характеристик продуктов одного товарного наименования связано с различием их химического состава (содержания влаги, белка, жира и сухих веществ).
Теплофизические характеристики зависят от температуры. При отсутствии фазовых переходов (отвердевания, плавления, льдообразования) эти изменения невелики. При переходе воды в твердую фазу эти изменения значительны, что связано с различием свойств воды и льда.
Вода - основной компонент сырья и готовых пищевых продуктов. Массовая доля воды колеблется в широких пределах: в растительных продуктах - от 80 % для груш до 95 % для помидоров и огурцов; в животных продуктах - от 50 % для жирной свинины до 78 % для говядины.
В пищевых продуктах вода содержится в виде растворов. Содержание в воде веществ, образующих с ней истинный раствор, обусловливает изменение ее характерных свойств: снижение температуры начала замерзания (криоскопической температуры), повышение температуры кипения и снижение давления водяного пара над раствором.
Криоскопическая температура подчиняется закону Рауля: понижение криоскопической температуры раствора tкр по сравнению с температурой замерзания чистого растворителя t0 (для воды t0 = 0 °С) пропорционально суммарной моляльной концентрации растворенных веществ. Коэффициент пропорциональности ω, называемый криоскопической постоянной, для воды равен 1,86 (кг · °С)/моль.
При температурах, равных криоскопической и ниже нее, образующиеся кристаллы льда практически не содержат растворенных веществ, поэтому при понижении температуры одно и то же количество растворенных веществ приходится на все меньшее количество воды; следовательно, концентрация раствора повышается и криоскопическая температура его понижается. Это приводит к тому, что вода в продукте вымораживается постепенно при понижении температуры. Таким образом, естественно появляется понятие доли вымороженной воды ω (tкр) как функции температуры. Безразмерная величина ω (tкр) имеет смысл доли содержащейся в продукте воды, которая переходит в лед при понижении температуры продукта до t. Очевидным образом функция ω имеет смысл лишь при t ≤ tкр, причем ω (tкр) = 0, поскольку при криоскопической температуре вода лишь начинает вымерзать.
Используя закон Рауля, можно просто получить явный вид функции ω (tкр). Действительно, при любой температуре t доля вымороженной воды должна быть такова, чтобы криоскопическая температура оставшегося раствора равнялась t. Но разность температур криоскопической и t0 пропорциональна моляльной концентрации растворенных веществ. Поскольку количество растворенных веществ остается неизменным, то эта концентрация, в свою очередь, обратно пропорциональна доле оставшейся незамерзшей воды, которая при температуре t равна 1 - ω (t), а при криоскопической температуре tкр равна 1. Таким образом, имеем
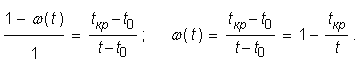
(1.2)
Выражение (1.2) просто и удобно, и им широко пользуются в холодильной технологии. Однако оно не вполне точное: опытные и расчетные значения ω различаются на 7... 10 %, причем наибольшее различие приходится на область низких температур.
ПРИМЕР.
Замораживается филе морского окуня от начальной температуры tнач = 20 °С до конечной tкон = -18 °С. Оценить количество теплоты, которое необходимо отвести от 1 кг продукта. Криоскопическая температура для морской рыбы tкр = -2 °С; влажность w = 0,8; доля незамерзающей воды 0,4; удельная теплоемкость незамороженного филе сн = 3500 Дж/(кг · К), замороженного - с = 1800 Дж/(кг · К).
Решение.
Теплота, отводимая от незамороженного филе:
Q1= cн(tнач – tкр) = 3500 · (20 – (–2)) = 77000 Дж/кг.
Доля вымороженной воды
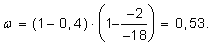
Теплота кристаллизации воды
Q3 = r · w · ω = 330000 · 0,8 · 0,53 = 140000 Дж/кг.
Теплота, отводимая от замороженной части,
Q3 = с (tкр – tкон) = 1800 · (–2 - (–18)) = 29000 Дж/кг.
Суммарная теплота
Q = Q1+ Q2 + Q3 = 246000 Дж/кг.

